Answer:
y=8/5x
Explanation:
Hi there!
We need to find the equation of the line that passes through (5,8) and the origin (the point (0,0)).
There are 3 ways to write the equation of the line, although the most common way is slope-intercept form, or y=mx+b where m is the slope and b is the y intercept
first, let's find m (slope)
The formula for the slope calculated from two points is
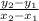 , where (
, where (
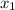 ,
,
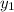 ) and (
) and (
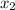 ,
,
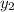 ) are points
) are points
we have two points, but let's label their values to avoid any confusion
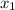 =5
=5
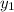 =8
=8
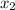 =0
=0
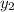 =0
=0
now substitute into the formula
m=
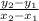
m=
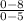
multiply
m=
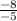
divide
m=8/5
The slope of the line is 8/5
here's the equation so far
y=8/5x+b
now we need to find b
as the point will pass through both (5,8) and (0,0) we can use either one of them to solve for b
let's take (0,0) as an example
substitute 0 as x and 0 as y
0=8/5(0)+b
multiply
0=0+b
add
0=b
substitute 0 as b into the equation
Therefore the equation of the line is:
y=8/5x (the 0 is not necessary)
Hope this helps! :)