Question

A student is given ZQUS ZRUT and the diagram and asked to prove m∠QOR = 56°. Given: ZQOS ROT Prove: m∠QOR = 56° Here is the student's proof: 1. given 2. m∠QOS = m∠ROT (definition of congruence) 3. m∠QOR + m∠ROS = m∠TOS + m∠ROS (angle addition) 4. m∠QOR = m∠TOS (subtraction property of congruence) 5. m∠TOS = 56° (given) 6. m∠QOR = 56° (subtraction property of equality) Where is the first error or skipped step in this proof?

Answer 1

The first error in the proof is in step 4, where the subtraction property of congruence is incorrectly applied.

Step-by-step explanation:

In step 4, the student incorrectly applies the subtraction property of congruence, stating that
`\( m\angle QOR = m\angle TOS \)`. The subtraction property of congruence is not a valid property for angles; it is used for segments or lengths. In this case, the student needs to recognize that
`\( m\angle QOR \) and \( m\angle TOS \)` are angles, not lengths. The correct step should involve subtracting
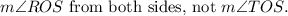`\( m\angle ROS \) from both sides, not \( m\angle TOS \).` This error leads to a flawed conclusion in step 6.

Additionally, the student could improve the clarity of the proof by providing reasons for each step. While the use of the subtraction property of congruence is incorrect, the student's understanding of congruence and angle addition is accurate up to that point.

The correct approach in step 4 should involve subtracting
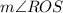`\( m\angle ROS \)` from both sides of the equation, maintaining the equality of
`\( m\angle QOR \) and \( m\angle TOS \)`. This would then align with the given information that
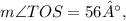`\( m\angle TOS = 56° \),`leading to the correct conclusion in step 6, where
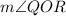`\( m\angle QOR \)` is indeed equal to 56°.