Question

X-17x^1/2+16=0
Solve using u-subsitution

Answer 1

x = 1 and x = 256

Explanation:

Given equation:

`x-17x^{(1)/(2)}+16=0`

To solve the given equation, we can use a substitution to simplify it.

`\textsf{Let}\;\;u=x^{(1)/(2)} \implies u^2=x`

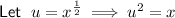
Therefore, the equation becomes:

`u^2-17u+16=0`

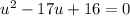
Now we have a quadratic equation that can be factored:

`\begin{aligned}u^2-17u+16&=0\\u^2-16u-u+16&=0\\u(u-16)-1(u-16)&=0\\(u-1)(u-16)&=0\end{aligned}`

Using the Zero Product Property, set each factor equal to zero and solve for u:

`u-1=0 \implies u=1`

`u-16=0 \implies u=16`

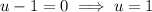
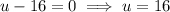
Substitute back in
`u=x^{(1)/(2)}`, and square both sides to solve for x

`\begin{aligned}x^{(1)/(2)}&=1\\\left(x^{(1)/(2)}\right)^2&=1^2\\x^{(2)/(2)}&=1\\x^1&=1\\x&=1\end{aligned}`
`\begin{aligned}x^{(1)/(2)}&=16\\\left(x^{(1)/(2)}\right)^2&=16^2\\x^{(2)/(2)}&=256\\x^1&=256\\x&=256\end{aligned}`

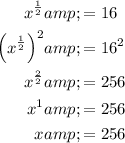
Therefore, the solutions to the given equation are x = 1 and x = 256.