Answer:
Approximately
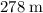 .
.
Step-by-step explanation:
The following SUVAT equation relates displacement
 to initial velocity
to initial velocity
 , final velocity
, final velocity
 , and acceleration
, and acceleration
 :
:
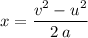 .
.
In this question:
- Final velocity:
 since the train has completed stopped.
since the train has completed stopped. - Initial velocity:
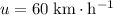 , which needs to be converted into the standard unit of meters per second.
, which needs to be converted into the standard unit of meters per second. - Acceleration:
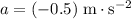 , which is negative since the train is slowing down.
, which is negative since the train is slowing down.
Apply unit conversion and ensure that all quantities are measured in standard units:
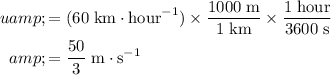 .
.
Substitute the value of
 ,
,
 , and
, and
 into the expression for
into the expression for
 to obtain:
to obtain:
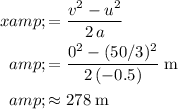 .
.