Question

In which quadrant does θ lie given that sinθ<0 and cosθ>0? responses quadrant i quadrant , roman numeral 1 quadrant ii quadrant , roman numeral 2 quadrant iii quadrant , roman numeral 3 quadrant iv

Answer 1

The angle θ lies in the fourth quadrant (IV).

Step-by-step explanation:

In the given scenario, sinθ is negative and cosθ is positive. This means that the angle θ lies in the fourth quadrant (IV) on the coordinate plane.

Answer 2

quadrant 1

The sine function is positive in the I & II quadrants.

The cosine function is positive in the I & IV quadrants.

This means the only quadrant that both trigonometric functions are positive is quadrant I.

Given that
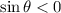`\(\sin \theta < 0\)` and
`\(\cos \theta > 0\)`, we can determine the quadrant in which the angle
`\(\theta\)` lies:

1.
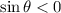`\(\sin \theta < 0\)` means that the sine of
`\(\theta\)` is negative. This occurs in the third and fourth quadrants since the sine function is negative in those quadrants.

2.
`\(\cos \theta > 0\)` means that the cosine of
`\(\theta\)` is positive. This occurs in the first and fourth quadrants since the cosine function is positive in those quadrants.

Therefore, the conditions
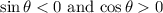`\(\sin \theta < 0\) and \(\cos \theta > 0\)` are satisfied in the fourth quadrant.

So,
`\(\theta\)` lies in the fourth quadrant.