Question

What is one solution to the trigonometric equation 3sinx − cos2x 3 = 0 in the interval [0, 2π]?

Answer 1

The solutions in the interval [0, 2π] for the equation
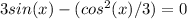`3sin(x) - (cos^2(x)/3) = 0` are approximately is x ≈ 0.469 radians and x ≈ 2.672 radians.

To solve the trigonometric equation
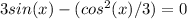`3sin(x) - (cos^2(x)/3) = 0` in the interval [0, 2π], you can follow these steps:

Step 1: Rewrite the equation to simplify it:

`3sin(x) - (cos^2(x)/3) = 0`

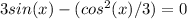
Multiply both sides of the equation by 3 to eliminate the fraction:

`9sin(x) - cos^2(x) = 0`

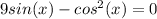
Step 2: Use the trigonometric identity
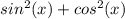`sin^2(x) + cos^2(x)` = 1 to replace
`sin^2(x)`:

`9(1 - cos^2(x)) - cos^2(x) = 0`

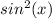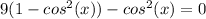
Step 3: Expand and simplify the equation:

`9 - 9cos^2(x) - cos^2(x) = 0`

Step 4: Combine like terms:

`-10cos^2(x) + 9 = 0`

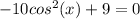
Step 5: Solve for
`cos^2(x)`:

`-10cos^2(x) = -9`

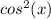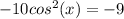
Divide both sides by -10:

`cos^2(x) = 9/10`

Step 6: Take the square root of both sides (remember to consider both positive and negative square roots):

cos(x) = ±√(9/10)

Step 7: Find the values of x in the interval [0, 2π] where cos(x) is equal to ±√(9/10).

First, find the values where cos(x) = √(9/10):

x = arccos(√(9/10))

Using a calculator to find the approximate value:

x ≈ 0.469 radians

Now, find the values where cos(x) = -√(9/10):

x = arccos(-√(9/10))

Using a calculator to find the approximate value:

x ≈ 2.672 radians

So, The answer is approximately x ≈ 0.469 radians and x ≈ 2.672 radians.

Answer 2

One solution to the trigonometric function is 330⁰.

How the solution to the function is determined.

Solution to the trigonometric equation 3sin(x) - cos2(x) + 3 = 0 in the interval [0, 2π] can be found as follows

3sin(x) - cos2(x) + 3 = 0

Substitute cos2(x) with 1 - 2sin²(x).

3sin(x) - (1 - 2sin²(x)) + 3 = 0

Simplify

3sin(x) - 1 + 2sin²(x) + 3 = 0

2sin²(x) - 3sin(x) - 2 = 0

Factor the quadratic equation

2sin²(x) - 3sin(x) - 2 = 0

(2sin(x) + 1)(sin(x) -2) = 0

Set each factor equal to zero and solve for SinX

2sin(x) + 1 = 0

Sin(x) = -1/2

Sine is negative in 3rd and 4th quarants

x = sin⁻¹(-1/2)

x = 330⁰

Also,

sin(x) -2 = 0

sin(x) = 2

This is not feasible because the values of sinx exist between -1 and 1.

One solution to the trigonometric function is 330⁰.