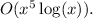Question

Find a big-O estimate of f(x)=(3x² + xlog(x²) + x²log(x²))·(πx³ + 2x + 4) + (x² + x⁴log(x)) such that in your estimate f(x) is O(g(x)) and g(x) is a simple function of the smallest order.

Answer 1

The function f(x) is O(x^7) because the term with the highest order in the given expression is x^4log(x) multiplied by πx^3, which simplifies to πx^7. Logarithmic factors are considered of lower growth compared to polynomial factors in Big-O notation.

Step-by-step explanation:

Finding a Big-O Estimate for a Function

To find a Big-O estimate for the function f(x) = (3x² + xlog(x²) + x²log(x²))·(πx³ + 2x + 4) + (x² + x´log(x)), we are looking for a simpler function g(x) such that f(x) is O(g(x)). When determining the Big-O complexity, we focus on the term with the highest growth rate because, as x approaches infinity, this term will dominate the overall growth rate of the function.

Within f(x), the term with the highest growth rate is x´log(x), multiplied by the highest order term from the polynomial, which is πx³. Multiplying these terms gives us πx⁷log(x), which simplifies to πx⁷ in the context of Big-O notation, since logarithmic factors are minor compared to polynomial factors as x approaches infinity. Therefore, the function g(x) we are looking for is x⁷, and we can say that f(x) is O(x⁷).

Answer 2

The Big O estimate for the function
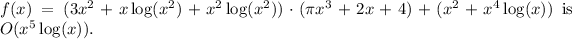`\( f(x) = (3x^2 + x\log(x^2) + x^2\log(x^2))\cdot(\pi x^3 + 2x + 4) + (x^2 + x^4\log(x)) \) is \( O(x^5\log(x)) \).` This means that for large values of
`\( x \), \( f(x) \)` grows at the rate of
`\( x^5\log(x) \).`

To find the Big O estimate of the given function
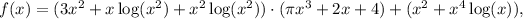`\( f(x) = (3x^2 + x\log(x^2) + x^2\log(x^2))\cdot(\pi x^3 + 2x + 4) + (x^2 + x^4\log(x)) \),` we need to simplify it in terms of its highest order term. Let's break it down step by step.

1. Simplify Each Component:

- First, let's simplify the components of the function:

-
`\( x\log(x^2) \) can be simplified to \( 2x\log(x) \) since \(\log(x^2) = 2\log(x)\).`

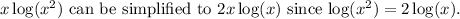
- Similarly,
`\( x^2\log(x^2) \) simplifies to \( 2x^2\log(x) \).`

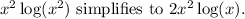
- The rest of the terms are already in their simplest form.

2. Expand the Product:

- Next, expand the product in the function:

`\[ (3x^2 + 2x\log(x) + 2x^2\log(x))\cdot(\pi x^3 + 2x + 4) \]`

- This will result in a sum of products, where each term will be a multiplication of terms from each bracket.

3. Identify the Highest Order Term:

- In the expanded form, the highest order term will dominate as x goes to infinity.

- The highest order term will come from the product of the highest order terms in each bracket. In this case, it's
`\( 2x^2\log(x) \cdot \pi x^3 \), which simplifies to \( 2\pi x^5\log(x) \).`

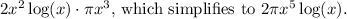
4. Consider the Other Terms:

- The function also has
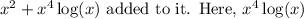`\( x^2 + x^4\log(x) \) added to it. Here, \( x^4\log(x) \)` is the dominant term.

- Comparing
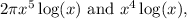`\( 2\pi x^5\log(x) \) and \( x^4\log(x) \),` the former is the highest order term because it has both a higher power of x and a logarithmic factor.

5. Big O Estimate:

- The Big O notation focuses on the highest order term for large values of x .

- Therefore, the Big O estimate of f(x) is the highest order term we identified, which is
`\( 2\pi x^5\log(x) \).`

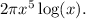
- However, for Big O notation, we often simplify the coefficient and constants. So the Big O estimate would be
`\( O(x^5\log(x)) \).`