Question

Evaluate
64 ^1/2 times by 10^-2
Give your answer as a fraction in its simplest form

Answer 1

2/25

Explanation:

(64) ^1/2 x 10 ^-2

√64 x 10⁻²

8 x 10⁻²

8 / 10²

8 / 100

2 / 25

Answer 2

`(2)/(25)`

Explanation:

To evaluate
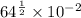`64^(\frac12) * 10^(-2)` and express the answer as a fraction in its simplest form, begin by rewriting 64 as 8²:

`(8^2)^(\frac12) * 10^(-2)`

`\textsf{Apply the power\;of\;a\;power exponent rule:}\quad (a^m)^n=a^(mn)`

`8^((2 \cdot\frac12)) * 10^(-2)`

`8^(1) * 10^(-2)`

`8 * 10^(-2)`

`\textsf{Apply the negative exponent rule:} \quad a^(-n)=(1)/(a^n)`

`8 * (1)/(10^2)`

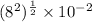
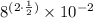
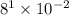
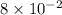
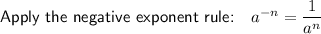
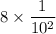
Evaluate 10²:

`8 * (1)/(100)`

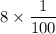
Rewrite 8 as a fraction with a denominator of 1:

`(8)/(1) * (1)/(100)`

`\textsf{Apply the fraction rule:} \quad (a)/(c)*(b)/(d)=(ab)/(cd)`

`(8)/(1) * (1)/(100)=(8 * 1)/(1 * 100)=(8)/(100)`

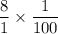
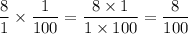
Now, simplify the fraction by dividing both the numerator and denominator by their greatest common factor (GCF), which is 4:

`(8/ 4)/(100/ 4) = (2)/(25)`

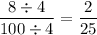
So,
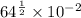`64^(\frac12) * 10^(-2)` simplifies to 2/25 as a fraction in its simplest form.