Question

Cynthia invested $12,000 in a savings account. If the interest rate is 6% per year, how much will be in the account in 10 years with quarterly compounding? Round your answer to the nearest cent.

Answer 1

After 10 years with quarterly compounding at an annual interest rate of 6%, Cynthia's savings account will have approximately $23,816.68.

Step-by-step explanation:

To calculate how much will be in Cynthia's savings account after 10 years with quarterly compounding at an annual interest rate of 6%, we will use the formula for compound interest, which is A = P(1 + r/n)^(nt), where:

• P is the principal amount (the initial amount of money)
• r is the annual interest rate (decimal)
• n is the number of times the interest is compounded per year
• t is the time the money is invested for, in years
• A is the amount of money accumulated after n years, including interest.

In this case, P = $12,000, r = 0.06 (6% expressed as a decimal), n = 4 (quarterly compounding), and t = 10 years.

Substituting these values into the formula gives us:

A = $12,000(1 + 0.06/4)^(4*10) = $12,000(1 + 0.015)^(40) = $12,000(1.015)^40

After calculating, we find A ≈ $12,000 * 1.9847235 ≈ $23,816.682, which, rounded to the nearest cent, is $23,816.68.

Therefore, the amount in the account after 10 years with quarterly compounding will be approximately $23,816.68.

Answer 2

After 10 years, with quarterly compounding at an annual interest rate of 6%, the amount in Cynthia's savings account will be $21,768.22.

To calculate the future value of Cynthia's investment with quarterly compounding interest, we'll follow these steps:

1. Understand the Formula:

The formula for compound interest is:

`\[ A = P \left(1 + (r)/(n)\right)^(nt) \]`

where:

- A is the amount of money accumulated after n years, including interest.

- P is the principal amount (the initial amount of money).

- r is the annual interest rate (decimal).

- n is the number of times that interest is compounded per year.

- t is the time the money is invested for in years.

2. Identify the Values:

- Principal, P = $12,000

- Annual interest rate, r = 6% = 0.06 (as a decimal).

- Number of times interest is compounded per year, n = 4 (quarterly compounding).

- Time in years, t = 10 .

3. Apply the Values to the Formula:

- We plug the values into the formula and calculate A :

`\[ A = 12000 \left(1 + (0.06)/(4)\right)^(4 * 10) \]`

4. Calculate the Future Value:

- Calculate the value inside the parentheses, then raise it to the power of 40 (since
`\( 4 * 10 = 40 \)).`

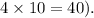
- Multiply the result by 12000 to find the total amount in the account after 10 years.

5. Round the Answer:

- Round the final answer to the nearest cent.

the amount in Cynthia's savings account will be $21,768.22.