Hello!
Answer:
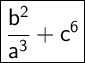
Explanation:
→ We want to simplify this expression:
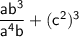
→ Simplify ab³/a⁴b:
→ Simplify b³/b:
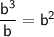
→ Simplify a/a⁴:
We know that
 is equal to
is equal to
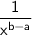

→ So:
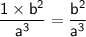
→ Simplify (c²)³:
We know that
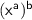 is equal to
is equal to
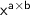
So:
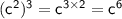
→ Simplify the expression:
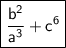
Conclusion:
The expression ab³/a⁴b + (c²)³ is equal to b²/a³ + c⁶.
So the answer is e).