Question

6) Factorise by using suitable identities 49p2 + 56pq + 16 q?​

Answer 1

To factorize the expression
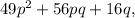`49p^2 + 56pq + 16q,` we can use the perfect square trinomial identity, which states that a^2 + 2ab + b^2 = (a + b)^2.

In this case, we can see that
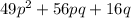`49p^2 + 56pq + 16q` can be factored as (7p + 4q)^2.The expression 49p^2 + 56pq + 16q can be factorized using the perfect square trinomial identity. The identity
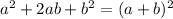`a^2 + 2ab + b^2 = (a + b)^2`applies here, where 'a' is 7p and 'b' is 4q.

We notice that
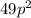`49p^2` is a perfect square of 7p, and 16q is a perfect square of 4q. Furthermore, 56pq can be seen as 2 times the product of 7p and 4q, which fits the 2ab term in the identity.

So, we rewrite the expression as
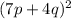`(7p + 4q)^2`, where
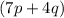`(7p + 4q)`is the common factor. This is the fully factorized form of the given expression, and it demonstrates how the expression can be expressed as the square of a binomial,
`7p + 4q`.