Question

The side of a square exceeds the side of another square by 3 cm, and the sum of the areas of the two squares is 549 cm². Find the perimeter of the larger square.

Answer 1

The side length of the smaller square is 15 cm and the perimeter of the larger square is 72 cm.

:

Let's denote the side length of the smaller square as x cm. Since the side of the larger square exceeds the side of the smaller square by 3 cm, the side length of the larger square is x + 3 cm.

The area of a square is given by the formula A = side^2. The sum of the areas of the two squares is 549 cm², so we can write the equation as follows:

x^2 + (x + 3)^2 = 549

Simplifying the equation, we get:

2x^2 + 6x - 540 = 0

Using the quadratic formula, we find that x = 15 or x = -18. Since the side length of a square cannot be negative, the side length of the smaller square is 15 cm.

The perimeter of a square is given by the formula P = 4 * side. Therefore, the perimeter of the larger square is 4 * (x + 3) = 4 * (15 + 3) = 4 * 18 = 72 cm.

Learn more about Perimeter of squares

Answer 2

Perimeter of larger square = 64 cm

Explanation:

Let the side of one square be 'x'.

The side of other square = (x + 3) cm

`\boxed{\text{\bf Area of square = side*side}}`

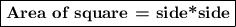
Finding the area of each square:

Area of square1 = x*x = x²

Area of square2 = (x+3) (x +3)

= (x + 3)²

Use algebraic identity (a + b)² = a² + 2ab + b²

= x² + 2*x*3 + 3²

= x² + 6x + 9

Factorizing the polynomials:

Sum of two squares = 549 cm²

x² + x² + 6x + 9 = 549

Combine like terms,

2x² + 6x + 9 = 549

2x² + 6x + 9 - 549 = 0

2x² + 6x - 540 = 0

Divide the entire equation by 2,

x² + 3x - 270 = 0

Sum = 3

Product = -270

Factors = 18 , (-15)

When we add 18 and (-15), we get 3 and when we multiply (-15) & 18, we get -270.

Rewrite the middle term using the factors.

x² + 18x -15x - 270 = 0

x(x + 18) - 15(x + 18) = 0

(x + 18)(x - 15) = 0

x + 18 = 0

x = -18 {Ignore as side of square cannot be a negative number}

x - 15 = 0

x = 15

Perimeter of larger square:

side = x + 3 = 15 + 3

= 18 cm

Perimeter of larger square = 4 * 18

= 64 cm

Answer: Perimeter of larger square = 64 cm