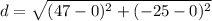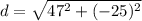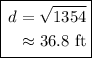Question

Please explain how to do it too​

Answer 1

a. (47, -25)

b.
`\approx 36.8 \text{ ft}`

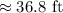
Explanation:

a.

If the center court is the origin, or (0, 0) on the coordinate plane, then the coordinates for the bottom right corner are:

• x: half of the length
• y: negative half of the width

This is because the length and width get distributed to:

• -(half length) to half length

instead of:

• zero to full length.

Calculating the x- and y-coordinates from the given dimensions:

• x = (1/2) × 94 ft
• y = (-1/2) × 50 ft

↓↓↓

• x = 47 ft
• y = -25 ft

So the ordered pair that represents the bottom right corner is:

(47, -25)

b.

We can find the distance that the ball has traveled using the distance formula from the origin (0, 0) to the bottom right corner (47, -25):

`d = √((c-a)^2+(d-b)^2)`

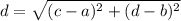
for the points
`(a, b)` and
`(c,d)`.

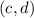We can name the following variable values:

• 
  `a = b = 0`
• 
  `c = 47`
• 
  `d = -25`

Plugging these into the formula and solving for distance:

`d = √((47-0)^2+(-25-0)^2)`

`d = √(47^2+(-25)^2)`

`\boxed{\begin{aligned}d = √(1354)\\ \approx 36.8 \text{ ft}\end{aligned}}`