Question

Raj’s bathtub is clogged and is draining at a rate of 1.5 gallons of water per minute. The table shows that the amount of water remaining in the bathtub, y, is a function of the time in minutes, x, that it has been draining. A 2-column table with 4 rows. The first column is labeled x with entries 0, 0.5, 1, 1.5. The second column is labeled y with entries 40, 39.25, 38.5, 37.75. What is the range of this function? all real numbers such that y ≤ 40 all real numbers such that y ≥ 0 all real numbers such that 0 ≤ y ≤ 40 all real numbers such that 37.75 ≤ y ≤ 40

Answer 1

The range of the function is all real numbers such that
`\(37.75 \leq y \leq 40\)`.

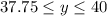The range, representing possible output values, is determined by the y-values in the given table. With a minimum of 37.75 and a maximum of 40, the range spans [37.75, 40], encompassing all possible water levels during the draining process.

The range of a function represents the set of all possible output values. In this scenario, the output values (y) are the amounts of water remaining in Raj's bathtub as it drains over time. The table provides a snapshot of this process at different time intervals.

Looking at the second column (y-values) in the table, we can observe that the minimum value is 37.75 and the maximum value is 40. Therefore, the range of the function is given by the interval [37.75, 40].

Now, let's interpret this result. The lower bound of 37.75 corresponds to the minimum amount of water remaining in the bathtub during the specified time intervals. As time progresses, the water level decreases, reaching this minimum value. On the other hand, the upper bound of 40 represents the initial amount of water in the bathtub. No matter how much time elapses, the water level will never exceed the initial amount. Therefore, the range of the function encompasses all real numbers within the interval [37.75, 40], capturing the complete variation in water levels during the draining process.