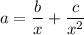Question

Ax² - bx - c = 0 Solve for a.
(literal equations 9th grade)

Answer 1

Explanation:

a x^2 - bx - c = 0 Add 'c' to both sides of the equation

a x^2 - bx = c Add 'bx' to both sides

ax^2 = c + bx Divide both sides by x^2

a = (c+bx) / x^2 Done.

Answer 2

`a=(bx+c)/(x^2)`

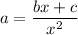
Explanation:

Given equation:

`ax^2-bx-c=0`

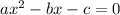
To solve for a, we need to isolate a on one side of the equation.

Add bx to both sides of the equation:

`\begin{aligned}ax^2-bx-c+bx&=0+bx\\ax^2-c&=bx\end{aligned}`

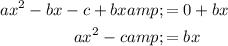
Add c to both sides of the equation:

`\begin{aligned}ax^2-c+c&=bx+c\\ax^2&=bx+c\end{aligned}`

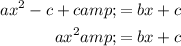
Divide both sides of the equation by x²:

`\begin{aligned}(ax^2)/(x^2)&=(bx+c)/(x^2)\\\\a&=(bx+c)/(x^2)\end{aligned}`

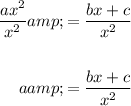
Therefore, the given equation solved for a is:

`\Large\boxed{\boxed{a=(bx+c)/(x^2)}}`

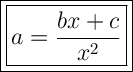
Additional comments

The right side of the equation can be separated into two fractions, by dividing bx by x² to give b/x, and dividing c by x² to give c/x²:

`a=(b)/(x)+(c)/(x^2)`