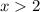Answer:
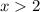
Explanation:
When given the following inequality;
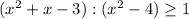
Rewrite in a fractional form so that it is easier to work with. Remember, a ratio is another way of expressing a fraction where the first term is the numerator (value over the fraction) and the second is the denominator(value under the fraction);
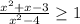
Now bring all of the terms to one side so that the other side is just a zero, use the idea of inverse operations to achieve this:

Convert the (1) to have the like denominator as the other term on the left side. Keep in mind, any term over itself is equal to (1);
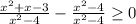
Perform the operation on the other side distribute the negative sign and combine like terms;
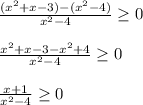
Factor the equation so that one can find the intervales where the inequality is true;
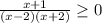
Solve to find the intervales when the equation is true. These intervales are the spaces between the zeros. The zeros of the inequality can be found using the zero product property (which states that any number times zero equals zero), these zeros are as follows;
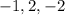
Therefore the intervales are the following, remember, the denominator cannot be zero, therefore some zeros are not included in the domain
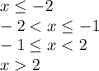
Substitute a value in these intervales to find out if the inequality is positive or negative, if it is positive then the interval is a solution, if it is negative then it is not a solution. This is because the inequality is greater than or equal to zero;
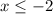 -> negative
-> negative
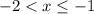 -> neagtive
-> neagtive
 -> neagtive
-> neagtive
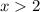 -> positive
-> positive
Therefore, the solution to the inequality is the following;