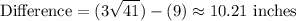Answer:
The difference between the two possible lengths for the third side of the triangle is about 10.21 inches.
Explanation:
We are given that the lengths of two sides of a right triangle is 12 inches and 15 inches.
And we want to find the difference between the two possible lengths of the third side.
In the first case, assume that neither 12 nor 15 is the hypotenuse of the triangle. Then our third side c must follow the Pythagorean Theorem:
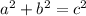
Substitute in known values:
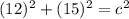
Solve for c:
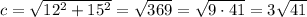
In the second case, we will assume that one of the given lengths is the hypotenuse. Since the hypotenuse is always the longest side, the hypotenuse will be 15. Again, by the Pythagorean Theorem:
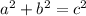
Substitute in known values:
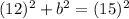
Solve for b:
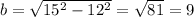
Therefore, the difference between the two possible lengths for the third side is: