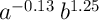Question

Simplify by expressing radicals as rational powers, combining powers where possible. Write the simplifed expression with no quotients. Enter your answers below. Round to two decimal places if necessary.

Answer 1

`\Large\text{$a^{-(1)/(8)}\: b^{(5)/(4)}$}`

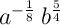
Explanation:

Given expression:

`\Large\text{$\frac{a^{-(7)/(8)}b^2}{a^{-(3)/(4)}b^{(3)/(4)}}$}`

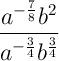
To simplify the given expression, we can use the Quotient Law of Exponents.

`\boxed{\begin{array}{c}\underline{\sf Quotient\;Law\;of\;Exponents}\\\\(a^m)/(a^n)=a^(m-n)\\\\\end{array}}`

The Quotient Law of Exponents states that when dividing terms with the same base, subtract the exponent in the denominator from the exponent in the numerator.

Therefore:

`\Large\text{$a^{\left(-(7)/(8)-\left(-(3)/(4)\right)\right)}\cdot b^{\left(2-(3)/(4)}\right)$}`

Simplify the exponents:

`\Large\text{$a^{\left(-(7)/(8)+(3)/(4)\right)}\cdot b^{\left(2-(3)/(4)}\right)$}`

`\Large\text{$a^{\left(-(7)/(8)+(6)/(8)\right)}\cdot b^{\left((8)/(4)-(3)/(4)}\right)$}`

`\Large\text{$a^{-(1)/(8)}\: b^{(5)/(4)}$}`

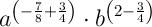
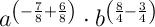
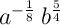
If the exponents should be decimals (rounded to two decimal places), then:

`-(1)/(8)=-0.125=-0.13\;\sf (2\;d.p.)`

`(5)/(4)=1.25`

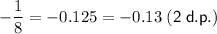
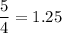
Therefore:

`\Large\text{$a^(-0.13)\: b^(1.25)$}`