Question

Let T : R^3 -> R^3: be a linear map defined by T(x,y,z) = (x+2y -> z,y + z.z + y-2y). Then what is the kernel of 7? A. KerT = x+2y – z=0. C. None of the choices in the list is correct. D. KerT = {a(3.-1.1) a E R] E. KerT = [(0.0.0)}:

Answer 1

The correct option is E: KerT = {(0, 0, 0)}.

Explanation:

It seems there might be some confusion in the notation and formatting in the given options. Let's clarify the situation:

You have a linear map T:
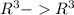`R^3 - > R^3` defined as:

T(x, y, z) =
`(x + 2y, z, y + z^2 - 2y)`

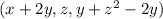
Now, you want to find the kernel of this linear map T, which consists of all vectors (x, y, z) in R^3 such that T(x, y, z) = (0, 0, 0).

So, we need to solve the following system of equations:

`x + 2y = 0z = 0y + z^2 - 2y = 0`

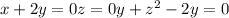
Let's solve each equation one by one:

From the first equation, we have x = -2y.

From the second equation, we have z = 0.

From the third equation, we have
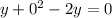`y + 0^2 - 2y = 0`, which simplifies to -y = 0, so y = 0.

Now that we have found x = -2y = 0 and z = 0, we can write the solutions in vector form:

(x, y, z) = (0, 0, 0)

So, the kernel of T is the set containing only the zero vector:

Ker(T) = {(0, 0, 0)}

Therefore, the correct option is E: KerT = {(0, 0, 0)}.