Question

Find the 14th term of the following geometric sequence. 2, 6, 18, 54, ... th Find the 12" term of the arithmetic sequence whose common difference is d=9 and whose first term is a = 2.

Answer 1

a₁₄ = 3188646 and a₁₂ = 101

Explanation:

the nth term of a geometric sequence is

`a_(n)` = a₁
`(r)^(n-1)`

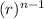
a₁ is the first term and r the common ratio

here a₁ = 2 and r =
`(a_(2) )/(a_(1) )` =
`(6)/(2)` = 3 , then

a₁₄ = 2
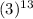`(3)^(13)` = 2 × 1594323 = 3188646

----------------------------------------------------------

the nth term of an arithmetic sequence is

`a_(n)` = a₁ + d(n - 1)

a₁ is the first term and d the common difference

here a₁ = 2 and d = 9 , then

a₁₂ = 2 + 9(11) = 2 + 99 = 101