Answer:
32.08
Explanation:
Formula to find any side length of a right triangle:
a^2 + b^2 = c^2
Where "a" and "b" represent legs/sides of a right triangle and "c" represents the hypotenuse, the longest side.
Plug in the side lengths and hypotenuse into this formula:
a^2 + b^2 = c^2
(5)^2 + b^2 = (14)^2
Solve, by finding exponents first:
25 + b^2 = 196
Get the variable, b, alone by subtracting 25 from both sides because the inverse operation of addition is subtraction:
25 + b^2 = 196
-25 -25
b^2 = 171
Square both sides since the inverse operation of squaring is finding the square root:
b^2 = 171
 =
=
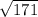
*Square root and squaring cancel out*
b = √171
Which is,
b = 13.0766968306
Round to the nearest hundredth:
b ≈ 13.08
Let's check our answer just in case:
a^2 + b^2 = c^2
5^2 + 13.08^2 = 14^2
25 + 171.1 = 196
196.1 ≈ 196
They are about the same, so 13.08 for one of the side lengths is correct.
Now let's find the perimeter by adding all the side lengths together:
5 + 13.08 + 14
= 32.08 is the perimeter.