Question

Find all solutions if 0° ≤ θ < 360°. Verify your answer graphically. (Enter your answers as a comma-separated list.) sin 2θ = √3/2 θ = ___

Answer 1

Final answer Answer:

The solutions are found by solving sin 2θ = √3/2. Initial solutions are 30°, 90°, and 120°, and considering the periodic nature of sine, valid solutions within 0° to 360° are 30°, 90°, and 120°. sin 2θ = √3/2 θ = 30°, 90°, 120°.

Explanation:

The equation sin 2θ = √3/2 can be solved by first finding the solutions for 2θ and then dividing by 2 to obtain the solutions for θ.

Let's solve for 2θ:

`\[sin 2θ = √(3)/2\]`

The reference angle for sin 60° is 60°. Therefore, 2θ = 60°, 180° - 60°, and 180° + 60° are the initial solutions.

1. \(2θ = 60° \implies θ = 30°\)

2. \(2θ = 180° - 60° \implies θ = 60°/2 \implies θ = 90°\)

3. \(2θ = 180° + 60° \implies θ = 240°/2 \implies θ = 120°\)

Now, we consider the periodic nature of sine, which repeats every 360°. Add 360° to the initial solutions to find additional solutions.

`4. \(θ = 30° + 360° = 390° \implies θ = 30°\)`

`5. \(θ = 90° + 360° = 450° \implies θ = 90°\)`

`6. \(θ = 120° + 360° = 480° \implies θ = 120°\)`

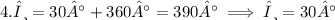
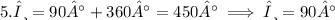
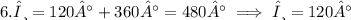
However, these solutions are beyond the given range of 0° to 360°. Therefore, the valid solutions for
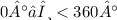`\(0° ≤ θ < 360°\)` are
`\(θ = 30°, 90°, 120°\)`.

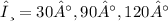To verify graphically, plot the function
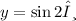`\(y = \sin 2θ\)` and the line
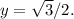`\(y = √(3)/2\).` The points of intersection represent the solutions. The graph should confirm the solutions obtained algebraically.

Answer 2

The solutions for the equation sin(2θ) = √3/2 in the given range 0° ≤ θ < 360° are 30° and 150°.

In order to find the solutions for the equation

sin(2θ) = √3/2 in the given range 0° ≤ θ < 360°,

we can use the double-angle identity for sine:

sin(2θ) = 2sin(θ)cos(θ). :

2sin(θ)cos(θ) = √3/2.

Now, since √3/2 is positive, either both sin(θ) and cos(θ) are positive, or both are negative.

Let's consider the positive case:

sin(θ)cos(θ) = √3/4.

sin(θ) = √3/2

θ = 60°,

so one solution is θ = 30°.

The other solution can be found by finding the angle whose sine and cosine multiply to give √3/4. In this case, θ = 150° is the other solution.

Therefore, the solutions for θ in the given range are 30° and 150°.