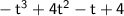Question

Multiply (t^2+1)(4-t)


i'm giving 50 points please help

Answer 1

Sure, I can help you multiply the expressions (t^2 + 1) and (4 - t). To do this, you can use the distributive property:

(t^2 + 1)(4 - t) = t^2(4 - t) + 1(4 - t)

Now, let's multiply each term:

t^2 * 4 = 4t^2
t^2 * (-t) = -t^3
1 * 4 = 4
1 * (-t) = -t

Now, combine the like terms:

4t^2 - t^3 + 4 - t

So, the product of (t^2 + 1) and (4 - t) is 4t^2 - t^3 + 4 - t.

Answer 2

`\sf -t^3 + 4t^2 -t +4`

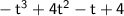
Explanation:

In order to multiply the expressions (t² + 1) and (4 - t), we can use the distributive property (also known as FOIL, which stands for First, Outer, Inner, Last).

Here's how to do it step by step:

`\sf (t^2 + 1)(4 - t)`

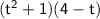
Multiply the terms in the first set of parentheses with the terms in the second set of parentheses:

`\sf First (F): t^2 * 4 = 4t^2`

`\sf Outer (O): t^2 * (-t) = -t^3`

`\sf Inner (I): 1 * 4 = 4`

`\sf Last (L): 1 * (-t) = -t`

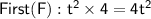
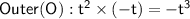
Now, add up all these results:

`\sf 4t^2 - t^3 + 4 - t`

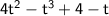
We can rearrange it as:

`\sf -t^3 + 4t^2 -t +4`

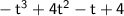
So, the product of (t²+ 1) and (4 - t) is:

`\sf -t^3 + 4t^2 -t +4`