The region enclosed by the curves
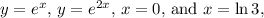 is
is

The integral for the area between the curves.
First, let's find the points of intersection of the curves
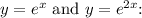
![\[ e^x = e^(2x) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/t754r41uzent2x78ktxh3fmqky0jcstwso.png)
Solving for x, we get
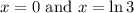 .
.
Now, the integral for the area between the curves is given by:
![\[ \text{Area} = \int_(a)^(b) \left|f(x) - g(x)\right| \,dx \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/46mp41sw0i1oyslv5e0tl4avuhck3nubet.png)
where a and b are the x-coordinates of the points of intersection.
In this case, the area is:
![\[ \text{Area} = \int_(0)^(\ln 3) \left|e^(2x) - e^x\right| \,dx \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/co5y3loe7hv8d71oxefhkrv798br3iz5cr.png)
Now, we can simplify this expression:
![\[ \text{Area} = \int_(0)^(\ln 3) (e^(2x) - e^x) \,dx \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/s9b9tb3aqgtu3ng9os1qxbetenx70ewuh6.png)
Now, integrate with respect to x:
![\[ \text{Area} = (1)/(2)e^(2x) - e^x \Big|_(0)^(\ln 3) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/pzb70hff3yos565b5mir7fbyny6sr5uln3.png)
Evaluate the expression at
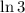 and subtract the value at 0:
and subtract the value at 0:
![\[ \text{Area} = (1)/(2)e^(2(\ln 3)) - e^(\ln 3) - \left((1)/(2)e^0 - e^0\right) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/ti5k3m0zanclh5r6nn6acsl4s97riynr7y.png)
![\[ \text{Area} = (1)/(2)(3^2) - 3 - \left((1)/(2) - 1\right) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/16myyfl4c8rnsts7ad0oyuqp7i78ips4na.png)
![\[ \text{Area} = (9)/(2) - 3 + (1)/(2) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/ldpwof1rsz6adhty5akajozsunj8242hoi.png)
![\[ \text{Area} = -(5)/(2) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/sa6pps46rejhwhnsa5anxowkvia11h8l6g.png)
So, the area of the region enclosed by the curves is
 Note that the negative sign indicates that the area is measured below the x-axis.
Note that the negative sign indicates that the area is measured below the x-axis.