2 Answers

Kirill Kovalevskiy · Answer 1 · 2024-05-25T01:51:31+0000

Explanation:

to raise a power to a power,raise each factor to that power. calculate the product.

Ben Harper · Answer 2 · 2024-05-28T19:08:09+0000

Hello!

Answer:

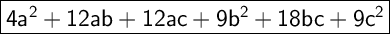
$\Large \boxed{\sf 4a^2 + 12ab+12ac+9b^2+18bc+9c^2}$

Explanation:

→ We want to simplify this expression:

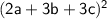
$\sf (2a +3b +3c)^2$

→ We know that
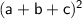$\sf (a+b+c)^2$ is equal to
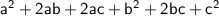$\sf a^2 + 2ab+2ac+b^2+2bc+c^2$ .

In our expression:

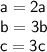
$\sf a = 2a\\b = 3b\\c = 3c$

→ So let's apply this formula:

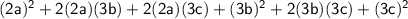
$\sf (2a)^2 + 2(2a)(3b)+2(2a)(3c)+(3b)^2+2(3b)(3c)+(3c)^2$

→ Simplify the expression:

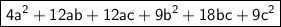
$\boxed{\sf 4a^2 + 12ab+12ac+9b^2+18bc+9c^2}$

Conclusion:

The expression (2a + 3b + 3c)² is equal to 4a² + 12ab + 12ac + 9b² + 18bc + 9c².

Please log in or register to add a comment.