Question

Factor the expression
12x^2 +7x+1

Answer 1

`\boxed{\textsf{ The factorised form is \textbf{(4x+1)(3x+1)}.}}`

Explanation:

A quadratic polynomial is given to us and we need to find its factorised form . The given quadratic polynomial is ,

`\sf\implies p(x)= 12x^2+7x+1`

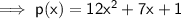
And this equation is similar to the equation in ax² + bx + c form . So in order to factorise it .

Step 1: Multiply the coefficient of x² with the constant term .

Here the coefficient of x² is 12 and the constant term is 1 . So on multiplying them we get 12*1= 12 .

Step 2: Look out for the possible factors of the number .

Here the obtained number is 12 . So the possible factors of 12 is

• 1 *12
• -1*-12
• 2*6
• -2*-6
• 4*3
• -4*-3

Step3: Choose the factor whose sum is equal to the coefficient of the middle term .

Here we can see that the middle term is 7 . And the sum of 4 and 3 is equal to 7 . Hence here we will break 7x as 4x + 3x .

Step 4: After proper arrangements take out the common term and then factorise.

After suitable rearrangment we get ,

`\sf\implies p(x)= 12x^2+4x+3x+1 \\\\\sf\implies p(x)= 4x(3x+1)+1(3x+1) \\\\\implies\boxed{\red{\sf p(x)= (4x+1)(3x+1)}}`