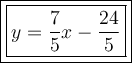Question

Find an equation of the tangent line to the graph of the equation x ^2 −y ^2 =24 at (7,5). (Use symbolic notation and fractions where needed.) Incorrect

Answer 1

`y=(7)/(5)x-(24)/(5)`

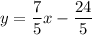
Explanation:

To find the equation of the tangent line to the graph of the equation x² - y² = 24 at the point (7, 5), we first need to find the slope of the tangent line at that point.

To do this, differentiate the equation implicitly with respect to x. This will give us the gradient of the tangent line in terms of x and y.

Begin by placing d/dx in front of each term of the equation:

`\frac{\text{d}}{\text{d}x}x^2-\frac{\text{d}}{\text{d}x}y^2=\frac{\text{d}}{\text{d}x}24`

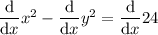
Differentiate the terms in x only (and constant terms):

`2x-\frac{\text{d}}{\text{d}x}y^2=0`

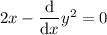
Use the chain rule to differentiate terms in y only.

In practice, this means differentiate with respect to y, and place dy/dx at the end:

`2x-2y\frac{\text{d}y}{\text{d}x}=0`

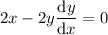
Rearrange to isolate dy/dx:

`2y\frac{\text{d}y}{\text{d}x}=2x`

`\frac{\text{d}y}{\text{d}x}=(2x)/(2y)`

`\frac{\text{d}y}{\text{d}x}=(x)/(y)`

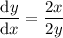
This is the gradient formula for the slope of the tangent line at any (x, y) point on the graph of x² - y² = 24.

Substitute the coordinates of the point (7, 5) into the gradient formula to find the slope (m) at that point:

`m=(7)/(5)`

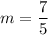
Now, substitute the found slope m = 7/5 and point (7, 5) into the point-slope form of a linear equation to write the equation of the tangent line.

`y-y_1=m(x-x_1)`

`y-5=(7)/(5)(x-7)`

`y-5=(7)/(5)x-(49)/(5)`

`y=(7)/(5)x-(24)/(5)`

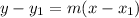
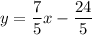
Therefore, the equation of the tangent line to the graph of x² - y² = 24 at the point (7, 5) is:

`\large\boxed{\boxed{y=(7)/(5)x-(24)/(5)}}`