Question

The left ventricle of the heart accelerates blood from the rest to a velocity of +23.8 cm/s.

(a) If the displacement of the blood during the acceleration is +1.72 cm, determine its acceleration (in cm/s^2).

(b) How much time does blood take to reach its final velocity?

Answer 1

(a) To determine the acceleration of the blood, you can use the following kinematic equation:

`v^2=u^2+2as`

Where:

• 
  `v` is the final velocity (23.8 cm/s)
• 
  `u` is the initial velocity (which is 0 cm/s because the blood starts from rest)
• 
  `a` is the acceleration (which we want to find)
• 
  `s` is the displacement (1.72 cm)

Now, plug in the given values:

`23.8^2 = 0^2 + 2a(1.72)`

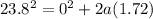
Simplify the equation:

`564.44 = 3.44a`

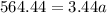
Now, solve for
`a`:

`a=(565.44)/(3.44)`≈
`164.09cm/s^2`

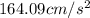
So, the acceleration of the blood is approximately
`164.09cm/s^2`

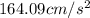
(b) To find the time it takes for the blood to reach its final velocity, you can use the following kinematic equation:

`v=u+at`

Where:

• 
  `v` is the final velocity (23.8 cm/s)
• 
  `u` is the initial velocity (0 cm/s)
• 
  `a` is the acceleration (164.09 cm/s^2, as calculated in part a)
• 
  `t` is the time (which we want to find)

Now, plug in the values:

`23.8=0+(164.09)t`

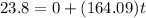
Solve for
`t`:

`t=(23.8)/(164.09)`≈
`0.145 s`

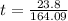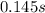
So, it takes approximately 0.145 seconds for the blood to reach its final velocity