Question

a straight line with slope -5 contains the point (1,2). what is the area of the triangle formed by this line and the x and y axes?

Answer 1

Answer: 4.9 square units

How to get this answer:

Apply point-slope form to determine the equation of this line.

`y - y_1 = m(x - x_1)\\\\y - 2 = -5(x - 1)\\\\y - 2 = -5x + 5\\\\y = -5x + 5+2\\\\y = -5x + 7\\\\`

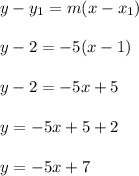
The y intercept is 7 which means the point (0,7) is on the line.

Let's find the x intercept. Replace y with 0 and solve for x.

`y = -5x + 7\\\\0 = -5x + 7\\\\5x = 7\\\\x = 7/5\\\\x = 1.4\\\\`

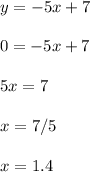
The x intercept is located at (1.4, 0)

The equation y = -5x+7, and the xy axis, intersect to form a triangle that has the vertex points (0,0) and (0,7) and (1.4, 0). Check out the diagram below.

This right triangle has: base = 1.4 and height = 7

Therefore,

area = 0.5*base*height = 0.5*1.4*7 = 4.9 square units