Answer:
↓↓↓
Explanation:
1. It's given that the slope is -6 and the line passes through the point (-14,14). So we can solve for the equation of the line, let's solve for it. Using the given slope and point, it would look like:
-6(-14) = 14
84 = 14
Now, obviously, 84 doesn't equal 14. This is just so we can figure out the y-intercept. Now, what would we need to subtract from 84 to get 14?
84 - 70 = 14
Now, plug it into the original equation.
-6(-14) - 70 = 14
84 - 70 = 14
Now we can say that the equation for the line is -6x - 70.
2. For this line, we aren't given a slope or y-intercept, only 2 points. Those 2 points are (-9,0) and (-4,4). But with these 2 points, we can figure out the slope, which we can then figure out the y-intercept.
If you don't know, slope is how many times y moves up or down divided by how many times x moves. Looking at the 2 points, we can see that going over 5 units makes the line go up 4 units. That would be
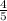 . Slope would be negative if we were going down 4 units, but since we're not, it's positive.
. Slope would be negative if we were going down 4 units, but since we're not, it's positive.
Now, like #1, let's use the slope and points to make an equation.
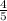 (-4) = 4
(-4) = 4
 = 4
= 4
Again,
 doesn't equal 0. So what do we need to add to
doesn't equal 0. So what do we need to add to
 to make it 4?
to make it 4?
 +
+
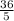 = 4
= 4
 = 4
= 4
Now, we think that the y-intercept is
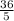 . To double check, we'll use the other point given.
. To double check, we'll use the other point given.
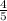 (-9) +
(-9) +
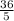 = 0
= 0
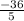 +
+
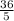 = 0
= 0
Now, we can say that the equation for the line is
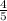 x +
x +
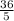 . Another way we can write that is 0.8x + 7.2.
. Another way we can write that is 0.8x + 7.2.