Question

How do you write an equation of a line with point (2,5), slope 5

Answer 1

Equation of a Line

<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<

Let's solve the problem given to us today! The problem is the following:

`\mapsto\quad\textbf{Write the equation of a line that has a slope of 5 and} \\\textbf{passes through the point (2,5).}`

__________________________________________________________

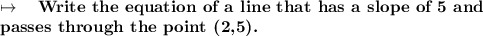
We will use the Point-Slope Equation for this.

__________________________________________________________

The point-slope formula is
`y-y_1=m(x-x_1)`.

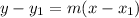Substitute the data:
`y-5=5(x-2)`

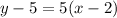
Use the distributive property on the right side:
`y-5=5x-10`

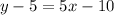
Add 5 to both sides:
`y=5x-5`

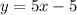
Therefore, the slope-intercept equation is y = 5x - 5.

<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<

Answer 2

y = 5x - 5

Explanation:

Let's use point slope formula:

y - y1 = m(x - x1)

Where "x1" and "y1" represent a set/pair of coordinates. And "m" represents the slope.

Given a pair of coordinates of:

(2, 5)

And a slope of:

5

Let's plug these values into our formula then get it into slope intercept form (y = mx + b, where y is dependent, x is independent, m is slope, and b is the point where the line intersects the y-axis (y-intercept.)):

y - y1 = m(x - x1)

y - 5 = 5(x - 2)

Distribute:

y - 5 = 5x - 10

Isolate "y" by adding 5 to both sides because the inverse property of subtraction is addition:

+5 +5

y = 5x - 5