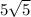Answer:
14.

16.
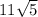
34.
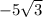
36.

38.
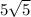
40.
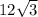
Explanation:
To add square roots, you must simplify/reduce them and add their like terms which are square roots with the same radicand (number under the square root symbol).
14.
Since their like terms are given (
 ), we just add the numbers beside them and keep the racidand the same.
), we just add the numbers beside them and keep the racidand the same.
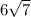 +
+
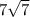
=

16.
The radiands are
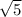 and
and
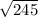 !
!
No problem, all we have to do is simplify
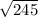 a little further.
a little further.
We can solve this multiple ways. In the way I use, we have to find 2 numbers that multiply to 245 but one of those factors has to be a perfect square (the multiplying of an integer by itself) and it has to be the GREATEST number it can be that goes into it. Then, you multiply them in the end. However, before you do that, you keep BOTH factors under radicals.
So two numbers that multiply to 245 (look at the factors of 245):
49 and 5, 49 is a perfect square so let's use it.
Put them both under radicals:
 ·
·
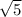 .
.
Square root of 49 can be simplified to 7 since 7 times 7 is 49.
Square root of 5 can not be simplified further so:
7 ·
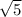
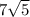
Now let's add
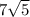 and
and
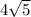 now that they both have like terms of square roots of 5.
now that they both have like terms of square roots of 5.
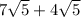
=
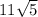
34.
They both have like terms so subtract them since the multiplicand 9 is negative.
Even though the negatives overrule the positives, still subtract the smallest from the largest number and keep the sign(-/+) that overrules, the same.

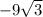
(4 + (-9)) --> get rid of " - " symbol to make easier (subtract smallest from largest without including the negative symbol of 9 to make it easier, 9 - 4 which is 5), sign that overrules is negative so, = -5.
=
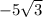
36.
The radicands are not the same (
 and
and
 ), let's apply what we did for no. 16 to this problem.
), let's apply what we did for no. 16 to this problem.
Since square root of 2 is simplified the furthest, we don't need to do anything with that radical. Though, the square root of 8 can be simplified.
Two numbers that multiply to 8 and one of the factors is a perfect square:
4 and 2, 4 is a perfect square.
Put them both under radicals:
 ·
·

Square root of 4 can be simplified to 2 since 2 times 2 is 4.
2 ·

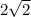
Now let's add
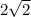 and
and
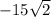 now that they both have like terms of square roots of 2.
now that they both have like terms of square roots of 2.
Basically, we're subtracting
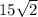 from
from
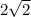 , and since the negatives overrule the positives, we keep the negative symbol. Now, subtract the smallest from the largest number, but get rid of negative symbol to make easier, (15 - 2 = 13). Put the negative symbol back: -13.
, and since the negatives overrule the positives, we keep the negative symbol. Now, subtract the smallest from the largest number, but get rid of negative symbol to make easier, (15 - 2 = 13). Put the negative symbol back: -13.
=

38.
The square roots are
 and
and
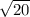 !
!
No problem, just simply both radicands.
Two numbers that multiply to 45 and have one factor that is a perfect square:
9 and 5, 9 is a perfect square.
Put them both under radicals:
 ·
·
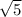
Square root of 9 can be simplified to 3 since 3 times 3 is 9.
3 ·
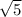
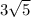
Now let's find the most reduced and simplified version of
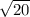 .
.
Two numbers that multiply to 20 and have one factor that is a perfect square:
4 and 5, 4 is a perfect square.
Put them both under radicals:
 ·
·
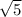
Square root of 4 simplifies to 2 since 2 times 2 is 4.
2 ·
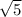
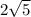
Now let's add these radicands:
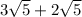
=