Answer:
D) Cannot be determined based on the information.
Explanation:
The given functions g(x) and f(x) are:
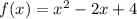
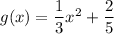
According to the given conditions, h(x) ≥ g(x) and h(x) ≤ f(x) for all values of x. This means that h(x) is bounded between g(x) and f(x) for all x.
Therefore:
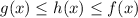
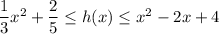
Consider the limit as x approaches 0 for g(x) and f(x):
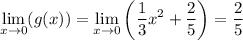


The Squeeze Theorem states that if h(x) is squeezed between f(x) and g(x) near
 , and if f(x) and g(x) have the same limit L at
, and if f(x) and g(x) have the same limit L at
 , then h(x) is trapped and will be forced to have the same limit L at
, then h(x) is trapped and will be forced to have the same limit L at
 also.
also.
As the limits of the two bounding functions are different, we cannot determine the limit of h(x) as x approaches 0 based solely on the information given.