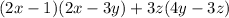Question

Factorise: 4x^2-4xy-3y^2+12yz-9z^2​

Answer 1

To factorize the expression
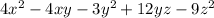`4x^(2) - 4xy - 3y^(2) + 12yz - 9z^2`, you can first look for common factors in pairs of terms. In this case, you can factor by grouping:

`4x^2-4xy-3y^2+12yz-9z^2=(4x^2-4xy-3y^2+(12yz-9z^2)`

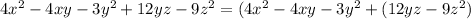
Now, let's factor each of these groups separately:

For the first group,
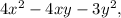`4x^2-4xy-3y^2,` you can factor it as follows:

`4x^2 - 4xy - 3y^2 = (4x^2 - 6xy+2xy-3y^2)=2x(2x-3y)-1(2x-3y)=(2x-1)(2x-3y)`

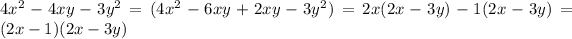
For the second group,
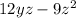`12yz-9z^2`, you can factor out the common factor of 3z:

`12yz - 9z^2 = 3z(4y-3z)`

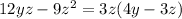
Now, you have factored in both groups:

`4x^2-4xy-3y^2+12yz-9z^2=(2x-1)(2x-3y)+3z(4y-3z)\\`

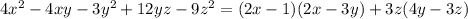
So, the fully factorized expression is
`(2x-1)(2x-3y)+3z(4y-3z)`