Question

Jake spent 1/4 of his net January salary on school fees. He spent 1/4 of the remainder on electricity and water bills. He spent 1/9 of what remained on transport. If he finally had sh. 3400 calculate his net January salary ​

Answer 1

Hello!

Answer:

`\Large \boxed{\sf 6800}`

Explanation:

→ We want to find his salary in January.

→ Let x be his salary in January.

→ His salary after paying the school fees is equal to:

`\sf x -( (1)/(4) ~of ~x) \\\\\\= x -( (1)/(4) * x) \\\\\\= x -(x)/(4) \\\\\\= (4x)/(4) - (x)/(4)\\\\\\= (3x)/(4)`

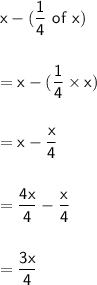
→ His salary after paying the electricity and water bills is equal to:

`\sf (3x)/(4) - ((1)/(4) ~of~(3x)/(4)) \\\\\\= (3x)/(4) -( (1)/(4) * (3x)/(4))\\\\\\= (3x)/(4) -(1 * 3x)/(4 * 4) \\\\\\= (3x)/(4) -(3x)/(16)\\\\\\= (12x)/(16) - (3x)/(16) \\\\\\= (9x)/(16)`

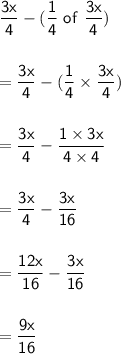
→ His salary after paying the transport bills is equal to:

`\sf (9x)/(16) - ((1)/(9)~ of~ (9x)/(16))\\\\\\= (9x)/(16) - ((1)/(9) * (9x)/(16))\\\\\\= (9x)/(16) - ((1 * 9x)/(9 * 16) )\\\\\\= (9x)/(16) - (9x)/(144) \\\\\\= (81x)/(144) - (9x)/(144)\\\\\\= (72x)/(144) \\\\\\= 0.5x`

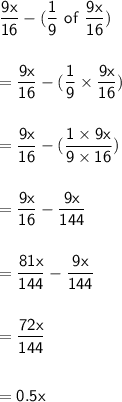
→ Now, we have this equation:

`\sf 0.5x = 3400`

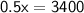
→ Let's solve this equation to find his salary in January:

◼ Divide both sides by 0.5:

`\sf 0.5x / 0.5= 3400/ 0.5`

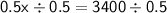
◼ Simplify both sides:

`\boxed{\sf x = 6800}`

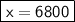
Check:

→ His salary after paying the school fees is equal to:

`\sf 6800 - ((1)/(4) ~of~ 6800)\\\\\\= 6800 - ((1)/(4) *6800)\\\\\\= 6800 - 1700\\\\\\= 5100`

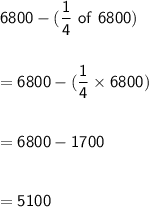
→ His salary after paying the electricity and water bills is equal to:

`\sf 5100 - ((1)/(4) ~of~ 5100)\\\\\\ = 5100 - ((1)/(4)* 5100)\\\\\\= 5100- 1275\\\\\\= 3825`

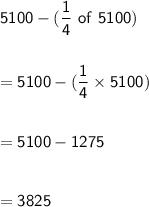
→ His salary after paying the transport bills is equal to:

`\sf 3825 - ((1)/(9) ~of~ 3825)\\\\\\ = 3825 - ((1)/(9)* 3825)\\\\\\= 3825- 425\\\\\\\boxed{\sf =3400}`

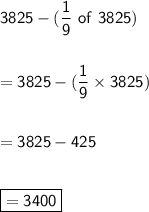
✓ So the check is good.

Conclusion:

The salary of Jack in January is 6800.