Question

How many coins 7cm in diameter and thickness 1cm must be melted to form a cuboid of dimensions 80cm × 15.4cm x 10cm?​

Answer 1

321 coins

Explanation:

To find out how many coins with a diameter of 7 cm and a thickness of 1 cm are needed to form a cuboid with dimensions of 80 cm × 15.4 cm × 10 cm, we need to calculate the volume of both the coins and the cuboid, and then divide the volume of the cuboid by the volume of a single coin.

Volume of one coin

The coin can be modelled as a cylinder.

The formula for the volume of a cylinder with radius r and height h is:

`\boxed{\textsf{Volume of a cylinder} = \pi r^2 h}`

The radius of a circle is half its diameter.

Given dimensions of a coin:

• Radius = Diameter / 2 = 7 cm / 2 = 3.5 cm
• Height = 1 cm

Substitute the values of r and h into formula to calculate the volume of a single coin:

`\begin{aligned}\textsf{Volume of a single coin}&= \pi \cdot (3.5)^2 \cdot 1\\&= \pi \cdot 12.25 \cdot 1\\&= 12.25 \pi\; \sf cm^3\end{aligned}`

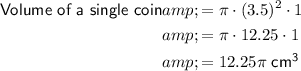
Volume of the cuboid

The formula for the volume of a cuboid with length l, width w and height h is:

`\boxed{\textsf{Volume of a cuboid} = l \cdot w \cdot h}`

Substitute the given dimensions into formula to calculate the volume of the cuboid:

`\begin{aligned}\textsf{Volume of the cuboid}&=80 \cdot 15.4 \cdot 10\\&=1232 \cdot 10\\&=12320\; \sf cm^3\end{aligned}`

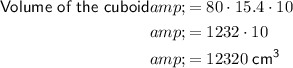
Number of coins needed

To find out how many coins are needed, divide the volume of the cuboid by the volume of a single coin:

`\begin{aligned}\textsf{Number of coins needed}& =\frac{\textsf{Volume of the cuboid}}{\textsf{Volume of a single coin}}\\\\&=(12320\; \sf cm^3)/(12.25\pi \; \sf cm^3)\\\\&=(12320)/(38.48451...)\\\\&=320.1287998...\end{aligned}`

Since we cannot have a fraction of a coin, we will need 321 coins with a diameter of 7 cm and a thickness of 1 cm to form a cuboid with dimensions 80 cm × 15.4 cm × 10 cm.