Question

144t² -49 please how to solve this math and what are the factors of that

Answer 1

Hello!

Answer:

`\Large \boxed{\sf (12t+7)(12t-7)}`

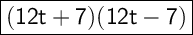
Explanation:

→ We want to factorize this expression:

`\sf 144t^2 - 49`

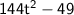
→ Our expression is equal to:

`\sf (12t)^2 - 7^2`

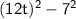
→ Let's use the difference of two squares:

`\sf a^2 - b^2 = (a+b)(a-b)`

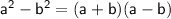
In our expression:

`\sf a = 12t\\b = 7`

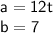
→ Let's apply this formula:

`\boxed{\sf (12t+7)(12t-7)}`

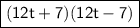
Conclusion:

The expression 144t² - 49 is equal to (12t + 7)(12t - 7).

Answer 2

there is nothing to solve, we can factorize

144t²-49 =a²-b² that we factor (a-b)(a+b)

a²= 144t², a = 12t

b² = 49, b= 7

144t² -49 = (12t-7)(12t+7)

we can solve 144t² -49 =0 but not ask in the statement

(12t-7)(12t+7)=0

12t-7=0⇔12t=7⇔t=7/12

(12t+7)=0⇔12t=-7⇔t=-7/12