Question

the incomplete data in the table above were recorded during an experiment in which two carts on a frictionless one-dimensional track collided head-on. what are the magnitudes of the average force

Answer 1

The magnitudes of the average force and average acceleration of Cart 2 are 260 N and
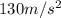`130 m/s^2` respectively.

How to solve

We can use the impulse-momentum theorem and the definition of average acceleration to solve for the required values.

1. Average Force (F_2):

Impulse on Cart 2 = (Final momentum - Initial momentum) = 2.00 kg * 8.0 m/s - (-5.0 m/s) * 2.00 kg = 26.0 kg m/s

Impulse on Cart 2 = Average force (F_2) * Time = F_2 * 0.10 s

Solving for F_2: F_2 = Impulse on Cart 2 / Time = 26.0 kg m/s / 0.10 s = 260 N

Therefore, the magnitude of the average force exerted on Cart 2 is 260 N.

2. Average Acceleration (a_2):

Average acceleration (a_2) = (Final velocity - Initial velocity) / Time = (8.0 m/s - (-5.0 m/s)) / 0.10 s =
`130 m/s^2`

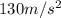
Therefore, the magnitude of the average acceleration of Cart 2 is 130 m/s^2.

The magnitudes of the average force and average acceleration of Cart 2 are 260 N and 130 m/s^2 respectively.

The Complete Question

Collision of Two Carts

THE TABLE

Cart Mass (kg) Initial Velocity (m/s) Final Velocity (m/s) Time (s) Average Force (N) Average Acceleration (m/s^2)

1 1.00 10.0 -2.0 0.10 ? ?

2 2.00 -5.0 8.0 0.10 ? ?

Given the data in the table, determine the following for Cart 2:

Average force (F_2): What is the magnitude of the average force exerted on Cart 2 during the collision?

Average acceleration (a_2): What is the magnitude of the average acceleration of Cart 2 during the collision?