425°
Explanation:
To find the coterminal angle for
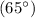 , We can add or subtract multiples of (360°) until we get an angle between (0°) and (360°).
, We can add or subtract multiples of (360°) until we get an angle between (0°) and (360°).
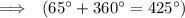
So, one coterminal angle is (425°).
To determine the quadrant, We can look at the original angle (65°):
- Quadrant I:
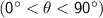
- Quadrant II:
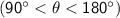
- Quadrant III:
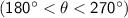
- Quadrant IV:
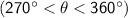
In this case, (65°) lies in Quadrant I.
Now, to find the reference angle, We can use the formula:
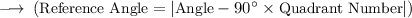
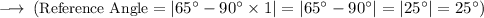
So, the coterminal angle is (425°), which lies in Quadrant I, with a reference angle of (25°).