Answer: -4
Step-by-step explanation
If you plug in x = 2, then what results is the indeterminate form 0/0.
To avoid this error, we rationalize the denominator.
Multiply top and bottom by

Here are the steps
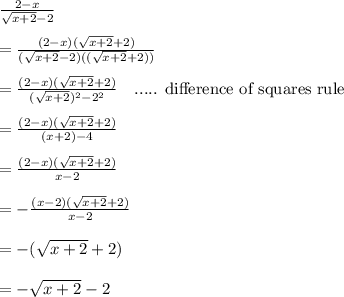
In short, we have the identity
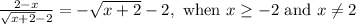
Put another way, the expression
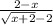 simplifies to
simplifies to
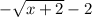
We can now evaluate the limit.
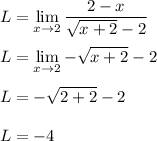
Therefore,
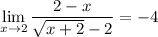
This can be confirmed with a graph. GeoGebra and Desmos are two options I recommend. Other tools like WolframAlpha can be used to confirm the answer.