Question

The midpoint of AB is M(1, 3). If the coordinates of A are (3, 1),

what are the coordinates of B?

Answer 1

The coordinates of B are (-1, 5)

Explanation:

A(3, 1) midpoint: M(1, 3)

Find what the coordinates of B are

Midpoint formula:
`((x_1+x_2)/(2) ,(y_1+y_2)/(2) )` where
`x_1,y_1` represents the coordinates of the first point and
`x_2,y_2` represent the coordinates of the second point.

`((3+x_2)/(2) ,(1+y_2)/(2) )=(1,3)`

Substitution

`((3+(-1))/(2) ,(1+(5))/(2) )=(1,3)`

Realize when you solve the equation, it is correct meaning the coordinates of B are (-1, 5)

Answer 2

B(-1,5)

Explanation:

Given that the midpoint of AB is M(1, 3) and the coordinates of A are (3, 1), we can find the coordinates of B using the midpoint formula.

The midpoint formula states that the coordinates of the midpoint of a segment with endpoints (x1,y1) and (x-2,y2) are:

`\sf M(x,y)=\left(( x_1 + x_2)/(2), (y_1 + y_2)/(2) \right)`

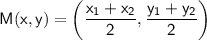
In this case:

we have:

M(x,y)=(1,3)

`\sf A(x_1,y_1)= (3,1)`

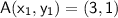
To find:

`\sf B(x_2,y_2)=`

Substituting value in the above formula:

`\sf M(1,3)=\left(( 3 + x_2)/(2), (1 + y_2)/(2) \right)`

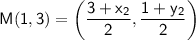
Now, comparing value,

`\sf 1= (3+x_2)/(2)`

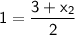
Multiply 2 on both sides

`\sf 1* 2 = 3+x_2`

`\sf 2 = 3+x_2`

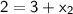
Subtract 3 on both sides:

`\sf 2 -3= 3+x_2-3`

`\sf x_2=-1`

Similarly:

`\sf 3= (1+y_2)/(2)`

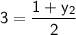
Multiply 2 on both sides

`\sf 3* 2 = 1+y_2`

`\sf 6 = 1+y_2`

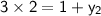
Subtract 1 on both sides:

`\sf 6-1 = 1+y_2-1`

`\sf y_2=-5`

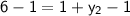
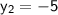
Therefore, the coordinates of B is (-1,5)