The probability that the mean diameter of the sample shafts would be greater than 206.3 inches is approximately 0.1271. This means that there is about a 12.71% chance that the sample mean would exceed 206.3 inches.
Given:
- Population variance
 = 6.25
= 6.25 - Population mean
 = 206 inches
= 206 inches - Sample size (n) = 90
- Desired mean
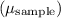 = 206.3 inches
= 206.3 inches
The sample mean follows a normal distribution when the sample size is large enough (central limit theorem).
Find the Standard Error of the Mean (SEM):
![\[\text{SEM} = (\sigma)/(√(n))\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/grwk0p23wbub38tnvqexxwkbvh2un589hh.png)
where
 is the population standard deviation.
is the population standard deviation.
Given
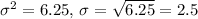 .
.
![\[\text{SEM} = (2.5)/(√(90)) = (2.5)/(9.4868) \approx 0.2636\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/to6a2p61ejon2oz66dwjokhg3xaq58f63v.png)
Calculate the Z-score:
The Z-score represents the number of standard errors the desired mean
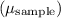 is from the population mean
is from the population mean
 .
.
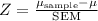
Given
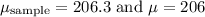 :
:
![\[Z = (206.3 - 206)/(0.2636) = (0.3)/(0.2636) \approx 1.1389\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/dtn2oq1cd2m02laehiq75h0p05rhwb3are.png)
Find the Probability using the Z-table or Calculator:
Using a standard normal distribution table or calculator, find the probability associated with the calculated Z-score.
The probability of getting a sample mean greater than 206.3 inches is the area to the right of the Z-score (since we're interested in the probability of the mean being greater).
Consulting a Z-table or calculator, the probability corresponding to
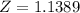 is approximately 0.1271.
is approximately 0.1271.
The probability that the mean diameter of the sample shafts would be greater than 206.3 inches is approximately \(0.1271\) when rounded to four decimal places.