Question

Content loaded for a free fall situation find the striking velocity for a 8 kg mass falls from 10 m height? a. 14 m/s. b. 7 m/s. c. 98 m/s. d. 196 m/s.d

Answer 1

Approximately
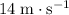`14\; {\rm m\cdot s^(-1)}` (assuming that
`g = 9.81\; {\rm m\cdot s^(-2)}`.)

Step-by-step explanation:

Under the assumption of free fall, the initial velocity of the object would be
`u = 0\; {\rm m\cdot s^(-1)}`, while the acceleration of the object would be
`a = g = 9.81\; {\rm m\cdot s^(-2)}`.

The acceleration of this object is constant, and the displacement (change in position) of the object is known. Hence, the velocity of the object after the acceleration can be found with the following SUVAT equation:

`\displaystyle v^(2) - u^(2) = 2\, a\, x`,

Where:

• 
  `v` is the velocity of the object after the acceleration,
• 
  `u = 0\; {\rm m\cdot s^(-1)}` is the initial velocity of the object,
• 
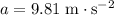  `a = 9.81\; {\rm m\cdot s^(-2)}` is the acceleration of the object, and
• 
  `x = 10\; {\rm m}` is the displacement of the object.

Rearrange this equation and solve for velocity
`v`:

`\begin{aligned}v &= \sqrt{u^(2) + 2\, a\, x} \\ &= √(2\, (9.81)\, (10))\; {\rm m\cdot s^(-1)} \\ &\approx 14\; {\rm m\cdot s^(-1)}\end{aligned}`.

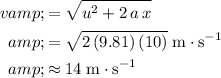In other words, the velocity of the object would be approximately
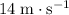`14\; {\rm m\cdot s^(-1)}` before it lands. Note that the mass of this object isn't required for these calculations. As long as the free fall assumptions are satisfied, the velocity of this object before the impact would not depend on the mass of the object.