Question

Which Radical Expressions Are Equivalent To 7^5/4?

a. 5√7
b. (∜7)⁵
c. ∜7⁵
d. (5√7)⁴
e. 5(√7⁴)
f. ∜7

Answer 1

The radical expression equivalent to 7^5/4 is ∜7⁵.

Step-by-step explanation:

The radical expression that is equivalent to 7^5/4 is given by option c. ∜7⁵. To understand why, we need to rewrite 7^5/4 as a radical expression. Since we know that x² = √x, we can express 7^5/4 as 7^(5/4). The exponent 5/4 represents the fourth root of 7 raised to the power of 5.

Answer 2

The equivalent radical expression to
`\(7^(5/4)\) is`option c. ∜7⁵.

Step-by-step explanation:

To determine the equivalent radical expression for
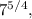`\(7^(5/4)\),` we first need to rewrite the exponent in terms of a root. The fractional exponent \(5/4\) represents the fourth root of \(7\) raised to the power of 5, expressed as \
`(\sqrt[4]{7^5}\).` The fourth root (∜) of
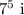`\(7^5\) i`s equivalent to
`\(7^(5/4)\).`

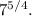
Let's evaluate the given options:

a. \(5√7\) represents the fifth root of \(7\), not the fourth root of
`\(7^5\).`

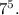
b. (∜7)⁵ signifies the fourth root of 7 raised to the power of 5, which equals
`\(\sqrt[4]{7^5}\).`

c. ∜7⁵ is the fourth root of \(7^5\) and simplifies to
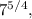`\(7^(5/4)\),` meeting the requirement.

d. (5√7)⁴ represents the fifth root of \(7\) raised to the power of 4, not the fourth root of
`\(7^5\).`

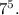
e. 5(√7⁴) signifies 5 times the fourth root of
`\(7^4\),` not the fourth root of \(7^5\).

f. ∜7 represents the fourth root of \(7\), not the fourth root of
`\(7^5\).`

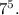
Therefore, upon evaluating the given options, it is evident that option c. ∜7⁵ represents the equivalent radical expression to \(7^{5/4}\), fulfilling the requirement.