Question

Solve the following system of equations using substitution:

Answer 1

x = 3 and y = -5

Explanation:

Given system of equations:

`\begin{cases}-2x-6y=24\\5x+3y=0\end{aligned}`

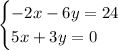
To solve the given system of equations using the method of substitution, solve one of the equations for one variable and then substitute it into the other equation.

Solve the first equation for y:

`\begin{aligned}-2x-6y&=24\\\\-2x-6y+2x&=24+2x\\\\-6y&=24+2x\\\\(-6y)/(-6)&=(24)/(-6)+(2x)/(-6)\\\\y&=-4-(x)/(3)\end{aligned}`

Substitute this into the second equation and solve for x:

`\begin{aligned}5x+3\left(-4-(x)/(3)\right)&=0\\\\5x-12-x&=0\\\\4x-12&=0\\\\4x-12+12&=0+12\\\\4x&=12\\\\(4x)/(4)&=(12)/(4)\\\\x&=3\end{aligned}`

Now that we have found the value of x, we can substitute it back into the equation we found for y:

`\begin{aligned}y&=-4-(3)/(3)\\\\y&=-4-1\\\\y&=-5\end{aligned}`

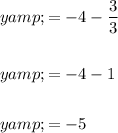
Therefore, the solution to the given system of equations is:

`\large\boxed{\boxed{x = 3\;\;\textsf{and}\;\;y = -5}}`