Question

I need help with parts b and c

Answer 1

b. Sample mean = 44.5

Sample standard deviation = 8.7

c. Sample mean = 3.5

Sample standard deviation = 0.7

Explanation:

Answer 2

`\textsf{(a)}\quad\overline{x}=42,\;\;s=8.2`

`\textsf{(b)}\quad\overline{x}=44.5,\;\;s=8.7`

`\textsf{(c)}\quad\overline{x}=3.5,\;\;s=0.7`

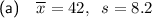
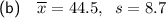
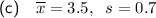
Explanation:

Part (a)

The formula for the sample mean
`\overline{x}` is:

`\large\boxed{\displaystyle\overline{x}=(\displaystyle\sum x_i)/(n)}`

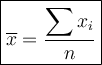
where:

• Each
  `x_i` is a data value.
• 
  `n` is the total number of data values.

Therefore, the sample mean of the given data set is:

`\overline{x}=(48+35+46+49+29+29+48+35+46+34+49+48+50)/(13)`

`\overline{x}=(546)/(13)`

`\overline{x}=42`

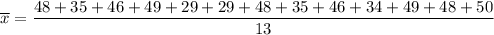
Therefore, the sample mean of the given data set is 42.

The formula for the sample standard deviation is:

`\boxed{s=\sqrt{\frac{\displaystyle\sum(x_i-\overline{x})^2}{n-1}}}`

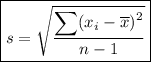
where:

• each
  `x_i` is a data value.
• 
  `n` is the total number of data values.
• 
  `\overline{x}` is the mean of the data set.

Calculate the sum of the squares of the differences between each data value and the mean:

`\begin{array}c\cline{1-3}x_i&x_i-\overline{x}&(x_i-\overline{x})^2\\\cline{1-3}48&48-42=6&36\\\cline{1-3}35&35-42=-7&49\\\cline{1-3}46&46-42=4&16\\\cline{1-3}49&49-42=7&49\\\cline{1-3}29&29-42=-13&169\\\cline{1-3}29&29-42=-13&169\\\cline{1-3}48&48-42=6&36\\\cline{1-3}35&35-42=-7&49\\\cline{1-3}46&46-42=4&16\\\cline{1-3}34&34-42=-8&64\\\cline{1-3}49&49-42=7&49\\\cline{1-3} 48&48-42=6&36\\\cline{1-3}50&50-42=8&64\\\cline{1-3}\sf Total&&802\\\cline{1-3}\end{array}`

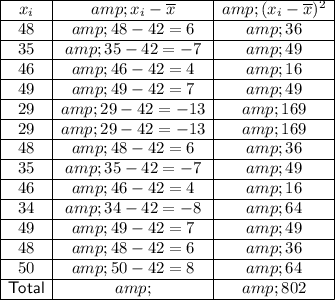
Substitute this into the sample standard deviation formula:

`s=\sqrt{(802)/(13-1)}`

`s=\sqrt{(802)/(12)}`

`s=8.17516564562...`

`s=8.2\; \sf (1\;d.p.)`

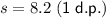
Therefore, the sample standard deviation of the given data set is 8.2 (rounded to one decimal place).

`\hrulefill`

Part (b)

As each employee in the sample is given a 6% raise, each revised data value will be 106% of the original data value. Therefore, the formula for the sample mean of the revised data set is:

`\overline{x}=(\displaystyle\sum 1.06\cdot x_i)/(n)`

`\overline{x}=(\displaystyle1.06\cdot\sum x_i)/(n)`

`\overline{x}=1.06\cdot(\displaystyle\sum x_i)/(n)`

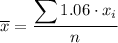
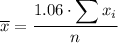
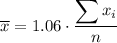
Therefore, to find the sample mean for the revised data set, we simply multiply the sample mean of the original data set by 1.06:

`\overline{x}=1.06\cdot 42`

`\overline{x}=44.52`

`\overline{x}=44.5\;\sf(1 \;d.p.)`

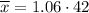
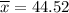
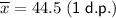
Therefore, the sample mean of the revised data set is 44.5 (rounded to one decimal place).

To calculate the revised salary sample standard deviation, first rewrite the formula. The revised data values and revised sample mean are the original data values
`(x_i)` and the original sample mean
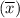`(\overline{x})` multiplied by 1.06:

`s=\sqrt{\frac{\displaystyle\sum(1.06x_i-1.06\overline{x})^2}{n-1}}`

`s=\sqrt{\frac{\displaystyle\sum(1.06(x_i-\overline{x}))^2}{n-1}}`

`s=\sqrt{\frac{\displaystyle\sum1.06^2(x_i-\overline{x})^2}{n-1}}`

`s=\sqrt{1.06^2\cdot\frac{\displaystyle\sum (x_i-\overline{x})^2}{n-1}}`

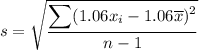
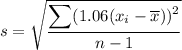
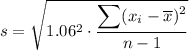
To find the sample standard deviation for the revised data set, substitute the sum of the square of the differences between each data value and the mean of the original data:

`s=\sqrt{1.06^2\cdot(802)/(13-1)}`

`s=\sqrt{1.1236\cdot(802)/(12)}`

`s=√(75.0939333...)`

`s=8.66567558...`

`s=8.7\; \sf (1\;d.p.)`

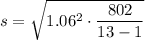
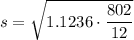
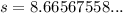
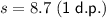
Therefore, the sample standard deviation of the revised data set is 8.7 (rounded to one decimal place).

`\hrulefill`

Part (c)

To calculate the monthly salary, we divide each original salary by 12.

Therefore, the monthly salary sample mean can be calculated by dividing the original sample mean by 12:

`\overline{x}=(42)/(12)=3.5`

Therefore, the monthly salary sample mean is 3.5.

To calculate the monthly salary sample standard deviation, first rewrite the formula. The original data values
`(x_i)` and the original sample mean
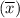`(\overline{x})` have been divided by 12, so:

`s=\sqrt{\frac{\displaystyle\sum\left((x_i)/(12)-\frac{\overline{x}}{12}\right)^2}{n-1}}`

`s=\sqrt{\frac{\displaystyle\sum\left(\frac{x_i-\overline{x}}{12}\right)^2}{n-1}}`

`s=\sqrt{\frac{\displaystyle\sum\frac{\left(x_i-\overline{x}\right)^2}{12^2}}{n-1}}`

`s=\sqrt{\frac{\displaystyle\sum\frac{\left(x_i-\overline{x}\right)^2}{144}}{n-1}}`

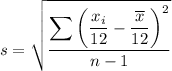
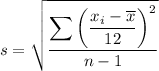
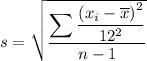
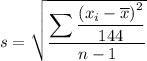
Therefore, with the rewritten formula, there is no need to calculate the sum of the squares of the differences separately. We can simply substitute the original value of
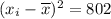`(x_i-\overline{x})^2=802` into the formula and solve:

`s=\sqrt{((802)/(144))/(13-1)}`

`s=\sqrt{(802)/(1728)}`

`s=0.681263803...`

`s=0.7\; \sf (1\;d.p.)`

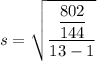
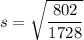
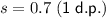
Therefore, the monthly salary standard deviation is 0.7 (rounded to one decimal place).