Answer:
B
Explanation:
First, we can see that the equation on the left is getting squared, and that we need it to equal a positive number. When any number is squared, no matter if it's positive or negative, it comes out positive.
Next, let's think of our perfect squares.
 = 1
= 1
 = 4
= 4
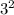 = 9
= 9
Now look back on the underlined sentence. So we now know that we need our equation on the left to equal either -3 or 3.
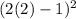 = 9
= 9
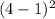 = 9
= 9
 = 9
= 9
9 = 9
Now we know that our positive number is 2. Let's look for our negative.
 = 9
= 9
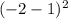 = 9
= 9
 = 9
= 9
9 = 9
Now we know that our x is both 2 and -1.