Answer:
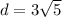
Explanation:
We can find the shortest distance between two points
 and
and
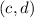 using the distance formula:
using the distance formula:
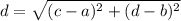
From the given points
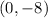 and
and
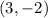 , we can identify the following variable values:
, we can identify the following variable values:
Plugging these into the formula and solving for distance:
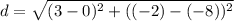
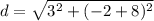
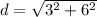


Finally, we can express the distance in simplest radical form by factoring the number under the square root and taking out any perfect squares.
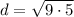
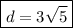
Further Note
The distance formula is just a manipulation of the Pythagorean Theorem. It basically models a right triangle with the two given points as vertices and solves for the hypotenuse.