Question

Which c value makes the expression x^2 + 8x + c a perfect square trinomial?

A. 32

B. 16

C. 4

D. 9

Answer 1

option B

16

Explanation:

x² + 8x + c

let c = 16

x² + 8x + 16

= x² + 4x + 4x + 16

= x(x + 4) + 4(x + 4)

= (x + 4)(x + 4)

= (x + 4)²

thus, c = 16 is the correct option

Answer 2

B. 16

Explanation:

A perfect square trinomial is a quadratic expression (a trinomial) that can be factored into the square of a binomial (a two-term expression).

A perfect square trinomial is in the form:

`\large\boxed{(a+b)^2=a^2+2ab+b^2}`

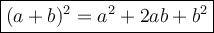
To make the given expression x² + 8x + c a perfect square trinomial, we need to find the value of c such that it can be written in this form.

Compare the given expression to the form of a perfect square trinomial:

`x^2 + 8x + c = a^2+2ab+b^2`

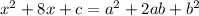
As x² = a², then a = x. Therefore:

`x^2 + 8x + c = x^2+2xb+b^2`

This means that 8x = 2xb.

Divide both sides by 2x to find the value of b:

`(8x)/(2x)=(2xb)/(2x) \implies 4=b`

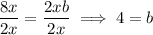
As c = b², and b = 4, then:

`c=4^2=16`

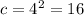
So, the correct value of c that makes x² + 8x + c a perfect square trinomial is:

`\Large\boxed{\boxed{\sf B.\;\;16}}`