Question

The Second Derivative Test cannot be used to conclude that x = 2 is the location of a relative minimum or relative maximum for which of the following functions? (A) f (x) = cos (– 2), where f'(x) = – sin(x – 2) - (B) f (x) = re , where f (x) = e 2 Na (C) f(x) = x2 – 4x – 2, where f'(x) = 2x – 4 (D) f (x) = x3 – 6x2 + 12x + 1, where f' (x) = 3x2 – 12x + 12

Answer 1

The location of a relative minimum or relative maximum for which of the following functions? is f(x) = x³ – 6x² + 12x + 1, where f' (x) = 3x² – 12x + 12.

The Second Derivative Test is used to determine the nature (concavity) of a critical point found by the First Derivative Test. It helps identify whether the critical point is a relative minimum, relative maximum, or neither.

The Second Derivative Test involves evaluating the sign of the second derivative at the critical point:

- If
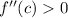`\(f''(c) > 0\)`, then
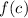`\(f(c)\)` has a relative minimum at \(x = c\).

- If
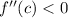`\(f''(c) < 0\)`, then
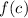`\(f(c)\)` has a relative maximum at \(x = c\).

Let's evaluate the second derivatives for the given functions:

`(A) \(f(x) = \cos(-2)\), where \(f'(x) = -\sin(x - 2)\):\\\[f''(x) = -\cos(x - 2)\]\\(B) \(f(x) = e^(2x)\):\\\[f''(x) = 4e^(2x)\]\\(C) \(f(x) = x^2 - 4x - 2\), where \(f'(x) = 2x - 4\):\\\[f''(x) = 2\]\\(D) \(f(x) = x^3 - 6x^2 + 12x + 1\), where \(f'(x) = 3x^2 - 12x + 12\):\\\[f''(x) = 6x - 12\]`

Now, evaluate \(f''(2)\) for each function:

`(A) \(f''(2) = -\cos(0) = -1\)\\(B) \(f''(2) = 4e^4 > 0\)\\(C) \(f''(2) = 2 > 0\)\\(D) \(f''(2) = 6(2) - 12 = 0\)`

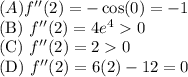
For option (D), since the second derivative test is inconclusive (the second derivative is zero), it cannot be used to conclude whether
`\(x = 2\)`is the location of a relative minimum or relative maximum for the function
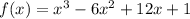`\(f(x) = x^3 - 6x^2 + 12x + 1\)`. Therefore, the correct answer is (D).